Thales teoremi (çember)

Bu madde çemberlerdeki bir teorem hakkındadır. Aynı adla anılan diğer teorem için Thales teoremi sayfasına bakınız.

Thales teoremi: eğer AC çapsa, B dik açıdır.

Çemberlerde Thales teoremi, alınan A, B ve C noktalarının bir çember üzerinde ve AC doğrusunun bu çemberin çapı olması durumunda, ABC açısının dik açı olacağını belirten geometri teoremi. Thales teoremi çevre açı kurallarının özel bir halidir. Adını Thales'ten alan teorem, genellikle ona atfedilir; ancak bazı yerlerde Pisagor'la da ilişkilendirilir.

İspat

Teoremin ispatı.

AC çap olduğu sürece, B açısı sabit ve dik açıdır.

Teoremin ispatında yararlanılacak kurallar:

• bir üçgenin iç açıları toplamı iki dik açıya (180°) eşittir,
• ikizkenar üçgenlerin taban açıları birbirine eşittir.

O çemberin merkezi olarak alınsın. OA = OB = OC olduğundan, OBA ile OBC birer ikizkenar üçgendir; ikizkenar üçgenin taban açılarının eşitliğinden, OBC = OCB ve BAO = ABO yazılır. α = BAO ve β = OBC diye adlandırılsın. ABC üçgenin iç açıları α, α + β ve β olacaktır. İç açılar toplamının iki dik açıya eşitliğinden

$\alpha +\left(\alpha +\beta \right)+\beta =180^{\circ }$

yani

${2}\alpha +{2}\beta =180^{\circ }$

ya da sadeleştirilirse

$\alpha +\beta =90^{\circ }$

QED

Tersi

Thales teoreminin evirilmiş hali de geçerlidir; yani bir dik üçgenin hipotenüsü, üçgenin çevrel çemberinin çapıdır.

Thales teoremiyle evirimi birleştirildiğinde elde edilecek ifade:

Bir üçgenin çevrel çemberinin merkezi, ancak ve ancak bir dik üçgen ise üçgenin kenarları üzerindedir.

Geometriyle ispatı

Evirmenin geçerliliğin ispatı

İspat dik üçgen dikdörtgene tamamlanarak ve dikdörtgenin merkezinin köşelere eşit uzaklıkta, dolayısıyla orijinal üçgenin çevrel çemberinin merkezi, olduğu göz önüne alınarak yapılır. İki bilgi kullanılır:

• bir paralelkenarın karşılıklı açıları bütünlerdir (toplamları 180°),
• bir dikdörtgenin köşegenleri eşit uzunluktadır ve birbirlerini orta noktalarında keserler.

ABC dik açısı, A'dan geçen BC'ye paralel r doğrusu ve C'den geçen AB'ye paralel s doğrusu alınsın. D r ile s doğrularının kesişim noktası olarak tanımlansın. (henüz D'nin çember üzerinde olduğu kesin değil)

Oluşan ABCD dörtgeni bir paralelkenardır (karşılıklı kenarları birbirine paralel). Paralelkenarın karşılıklı açıları bütünler (toplamları 180°) ve ABC açısının dik açı (90°) olduğu bilindiğinden BAD, BCD ve ADC açıları da diktir; yani ABCD bir dikdörtgendir.

AC ve BD köşegenlerinin kesişim noktası O olsun. O noktası, yukarıdaki ikinci bilgiye göre, A, B ve C köşelerine eşit uzaklıktadır. Bu durumda O çevrel çemberin merkezi ve üçgenin hipotenüsü AC çemberin çapı olur.

Lineer cebirle ispatı

İspat için iki bilgi kullanılacaktır:

• iki doğru arasında ancak ve ancak doğrultu vektörlerinin skaler çarpımı sıfırsa, dik açı bulunur
• bir vektörün boyutunun karesi, vektörün kendisiyle skaler çarpımıyla bulunur.

ABC dik açısı ve AC çaplı M çemberi alınsın. İşlemlerin basitleşmesi için M'in merkezi orijinde kabul edilsin. Buna göre

• A = − C, çünkü AC çaplı çemberin merkezinde orijinde ve
• (A − B) · (B − C) = 0, ABC dik açı.

İfadeler düzenlenirse

0 = (A − B) · (B − C) = (A − B) · (B + A) = |A|² − |B|².

Sonuçta:

|A| = |B|.

Yukarıdaki bağıntıya göre A ile B orijine, diğer bir ifadeyle M 'nin merkezine, eşit mesafededir. A 'nın M üzerinde olduğu düşünüldüğünde, B de çember üzerinde yer alacaktır ve bu durumda M çemberi üçgenin çevrel çemberidir.

Yapılan tüm işlemler Thales teoreminin, her iki yönde de, herhangi bir iç çarpım uzayında geçerli olduğunu gösterir.

Uygulamaları

Thales teoremi kullanılarak teğet çizimi.

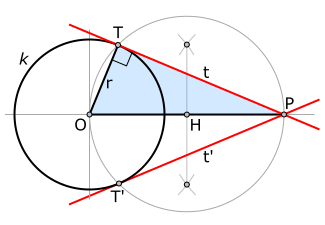
Thales teoremi yardımıyla bir çembere istenilen noktadan teğet çizilebilir. (Şekilde gösterildiği gibi) O merkezli bir k çemberi ve çember dışında bir P noktası alınarak, k 'ye P 'den geçen teğet(ler) (kırmızı) çizilmek istensin. Teğet doğrusu t ' çembere T noktasında değdiğini varsayalım (henüz bu bilinmiyor). Yarıçap OT teğete dik olacaktır. Sonrasında O ile P 'nin orta noktasına H diyerek, O ile P 'den geçen H merkezli bir çember çizelim. Thales teoremine göre, istenen T noktası iki çemberin kesişim noktasıdır; çünkü k üzerinde bulunur ve OTP dik üçgenini tamamlar.

Çemberlerin iki kesişimi olduğundan, bu yöntemle istenen noktadan geçecek iki teğet doğrusu da çizilebilir.

Tarihçe

Mısırlılar ve Babilliler'in ampirik olarak Thales teoremini biliyor olmaları gerektiği düşünülmekte olduğundan, Thales bu teoremi ilk bulan kişi değildir; ancak halkların teoremi ispatladığına dair herhangi bir kayıt yoktur. Teorem, Thales'in ikizkenar üçgenlerin taban açıları ve üçgenin iç açılarının toplamı gibi kendi çıkarımlarını kullanarak ispatı yapan ilk kişi olması nedeniyle, onun ismini almıştır.

Ayrıca bakınız

• Çevre açı
• Sentetik geometri

Kaynakça

• Agricola, Ilka (2008). Elementary Geometry. AMS. s. 50. ISBN 0821843478. 
• Heath, T.L. (1921). A History of Greek Mathematics: From Thales to Euclid. I. Oxford. s. 131. 

Dış bağlantılar

• Eric W. Weisstein, Thales teoremi (MathWorld)