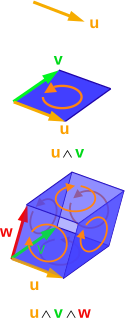
Tensör

Cauchy stres tensörü, ikinci-derece bir tensördür. Tensör bileşenlerinin,üç-boyutlu Kartezyen koordinat sistem matris formu:
${\begin{aligned}\sigma &={\begin{bmatrix}\mathbf {T} ^{(\mathbf {e} _{1})}\mathbf {T} ^{(\mathbf {e} _{2})}\mathbf {T} ^{(\mathbf {e} _{3})}\\\end{bmatrix}}\\&={\begin{bmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}\\\end{aligned}}$
sütuna etki eden gerilme (birim alan başına kuvvetleri) bulunmaktadır e₁, e₂ ve e₃ kübün yüzleri.

Matematikte, tensör, çok boyutlu verinin simgelenebildiği geometrik bir nesnedir. Skaler denilen yönsüz nicel büyüklükler, vektör denilen yönlü büyüklükler ve matris denilen iki boyutlu nesneler birer tensördür. Tensör, tüm bu nesnelerin genelleştirilmiş halidir ve çok boyutlu veri kümeleri için kullanılır. Nesnenin kaç boyutla ifade edildiğine de tensörün derecesi denilir. Bir skalerin derecesi sıfır, bir vektörün bir, bir matrisin ise ikidir. Tensörler üç ve üzeri dereceye sahip olabilir.

Bir tensör vektörler, skaler büyüklükler ve diğer tensörler arasındaki doğrusal ilişkileri ifade etmekte kullanılır. Bu tür ilişkilerin temel örnekleri arasında nokta çarpım, çapraz çarpım ve doğrusal dönüşüm vardır. Örneğin, Cauchy gerilme tensörü T girişi olarak bir v yönü alır ve T^(v) gerilmesini üreten giriş ve çıkış böylece şekilde (sağ) gösterilmiştir, iki vektör arasında bir ilişkinin ifade edilmesi için bu vektör, normal yüzeyinde bulunur, tensörlerin kendisi koordinat sisteminin belirli bir seçiminden bağımsız olmalıdır.

Bir koordinat veya referans çerçevesi alınması ve bu taban'da tensör veya referans çerçevesi'ni temsil eden organize birçok boyutlu dizi sonuçlarına tensör uygulamasına "kovaryant" dönüşüm denir. Bir tensörün koordinat bağımsızlığı daha sonra hesaplanmis başka bir koordinat sisteminde ilgili dizi formunu alır. Bu dönüşüm yasası bir geometrik veya fiziksel ortamda bir tensör kavramı içine yerleştirilmiş olarak düşünülmektedir ve dönüşüm yasasının kesin formunun tipini(veya değerliğini) belirler.

Tensör bu tür esneklik, akışkanlar mekaniği ve genel görelilik gibi alanlarda fizik problemlerini formüle etmek, çözmek ve kısa ve öz bir matematiksel çerçeve sağlamak için fizikte önemlidir. Tensörler ilkin mutlak diferansiyel hesapin bir parçası olarak Bernhard Riemann veElwin Bruno Christoffel ve diğerleri ve daha önceki çalışmalara devamla Tullio Levi-Civita ve Gregorio Ricci-Curbastro tarafından düşünülmüştür. Kavram Riemann eğrilik tensörü'nün içinde bir manifold şeklinde içsel diferansiyel geometri'sinin etkin alternatif formülasyonudur.

Tarihçe

Carl Friedrich Gauss diferansiyel geometri sonrasì çalışmalarında tensör analizi kavramlarıni ortaya attı ve formülasyon on dokuzuncu yüzyılın ortalarında cebrik form'ların teorisi ve değişmezlik geliştirilmesinden çok etkilenmiştir .. " Tensör " kelimesinin farklı bir şeyi açıklamak için tensörün ne anlama geldiği William Rowan Hamilton'un kendisi tarafından 1846 yılında tanımlandi. çağdaş kullanımı 1898 yılında Woldemar Voigt tarafından getirildi 'mutlak diferansiyel hesap' başlığı altında Gregorio Ricci - Curbastro tarafından 1890 civarında geliştirilen tensör hesabı ve orijinal sunumu 1892 yılında Ricci tarafından takdim edildi .. Tullio Levi-Civita's 1900 classic text Méthodes de calcul différentiel absolu et leurs applications (mutlak diferansiyel hesap yöntemleri ve uygulamaları) .

20. yüzyılda, konu tensör analizi olarak bilinir hale geldi ve 1915 civarında Einstein'ın genel görelilik teorisine giriş ile geniş bir kabul gördü. Genel görelilik tensörlerin dilinde tamamen formüle edilmiştir. Einstein geometrici Marcel Grossmann'dan gelen, büyük zorluklarla, onlar hakkında öğrendim. Levi - Civita sonra Einstein tensör analizi onun kullanımı ve yaptığı hataları düzeltmek için Einstein ile bir yazışma başlattı. Yazışmalar 1915-1917 arası sürdü ve karşılıklı saygı ile karakterize edilmiştir :

Ben hesaplama yönteminizin zarafetine hayran kaldım,bizim gibi zahmetle yürüyerek yolumuza yapmak varken doğru matematik atı üzerine binmek bu alanlar için güzel olmalı . -

— Albert Einstein, ,Görelilik İtalyan Matematikçiler

Tensörlerin, aynı zamanda, süreklilik mekaniği gibi diğer alanlarda yararlı olduğu bulunmuştur. Diferansiyel geometri tensörleri içinde iyi bilinen bazı örnekler metrik tansör'lerin karesel formları gibi ve Riemann eğrilik tensörü vardır.Hermann Grassmann'ın dış cebir'i, on dokuzuncu yüzyılın ortalarından itibaren, kendisi bir tensör teorisi ve son derece geometrik olduğunu, ancak doğal olarak tensör hesabı ile birleşik diferansiyel form'larının teorisi ile, görülen önce biraz zaman önce oldu. Elie Cartan çalışmaları ile matematikte kullanılan tensörlerin temel türlerinden bir diferansiyel formlar inşa etti 1920'lerden itibaren hakkında, bu tensör (örneğin Künneth teoremi) cebirsel topolojide temel bir rol oynadığını gerçekleşmiştir. Buna karşılık özellikle Homolojik cebir,soyut cebir birçok branşta çalışan tensörlerin tipleri ve temsil teorisi vardır . Çoklulineer cebir bir alan'dan gelen skalarlar için daha büyük genelliği içinde gelişmiş olabilir, ancak teori kesinlikle daha az geometrik ve daha teknik ve daha az algoritmik hesaplama içerir. Tensörleri monoidal kavramı vasıtasıyla kategori teorisi içinde 1960'lardan beri jeneralizedir.

Tanım

Tensörleri tanımlayan çeşitli yaklaşımlar vardır. Görünüşte farklı olmalarına rağmen, sadece farklı düzeylerde soyutlama ve farklı dilleri kullanarak aynı geometrik kavramını tanımlama yaklaşımlarıdır.

Çok boyutlu diziler olarak

Skaler tek bir numara ile tarif edilir ve belirli bir tabana göre verilen bir vektör bir boyutun bir dizisi tarafından tanımlanıyor, bir taban ile ilgili herhangi bir tensör çok boyutlu bir dizi ile tarif edilmektedir.

Dizideki sayılar tensörünün skaler bileşenleri ya da sadece bileşenleri olarak bilinir. Tensörün sembolik isminden sonra, altsimge ve üstsimge gibi, dizide ifade edilen indisler konumları verilerek gösterilir. Çoğu durumda, bir tensörün indisleri ya eşdeğişken veya karşıtdeğişkendir, sırasıyla alt simge veya üst simge ile belirlenmiştir Benzersiz her bileşeni seçmek için gerekli indislerinin toplam sayısı dizinin boyutuna eşittir ve tensörün sırası, derece veya seviyesi denir. Örneğin, bir 2 sıralı T tensörün girişleri i ve j ile ilgili vektör uzayının boyutuna 1'den çalışan indisleri T_ij, T_i ^j, Tⁱ_j veya T^ij, ifadesi olacaktır.

Taban ve (yani bir ortonormal baz için) onun ikili çakışığı, karşıtdeğişken ve eşdeğişken arasındaki fark bildirdiğinden indisler o zaman göz ardı edilebilir; Bu durum içindeT_ij veya T^ijbirbirinin yerine kullanılabilir olabilir Siz sadece bir vektör değişim bileşenlerinin vektör uzay tabanını değiştirmek gibi bir tensörün girişlerini de böyle bir dönüşüm yasası altında değiştirebilirsiniz. Bir taban değişimi karşı tensörün bileşenlerinin nasıl yanıt detayı olacağı bir dönüşüm yasası ile donatılmış her tensör olarak geliyor. Bir vektörün bileşenlerinin yeni taban vektörleri $\mathbf {\hat {e}} _{i}$ eski baz vektörler $\mathbf {e} _{j}$ cinsinden ifade edilir bazda bir değişime (vektörlerin vektörlerin eşdeğişken ve karşıdeğişken'ine bakınız), iki ayrı şekilde cevap verebilir.

Tensör hesabı

Matematikte, tensör hesabı veya tensör analizi tensör alanları (uzay boyunca ve zaman'la değişen tensör) olarak adlandırılan daha genel matematiksel nesnelere vektör analizinin gelişmiş bir uzantısıdır. Tensor hesabının gerçek-hayatta uygulamaları çoktur Fizik'te ve mühendislik'te stres analizi dahil, süreklilik mekaniği,elektromanyetizma (bakın elektromanyetik alanın matematiksel açıklamaları) ve genel görelilik)(bakın Genel görelilik matematiği)

Örnekler

Ayrıca bakınız: Dyadic tensör

Vectors (u, v, w) exterior-multiplied to obtain n-vectors (parallelotope elements).

1-forms (ε, η, ω) exterior-multiplied to obtain n-forms ("meshes" of coordinate surfaces, here planes)

n vektörlerin dış çarpım'larının Geometrik yorumu için ve n 1-form'lar, burada n eğim'dir, for n = 1, 2, 3. The "circulations" show orientation.

Bu tabloda tensörlerin önemli örnekleri gösterilmiştir. Her iki tensör dahil olmak üzere vektör uzayları ve tensör alanları olarak manifoldlar. Tensör kendi türüne göre sınıflandırılır (n, m). örneğin, bir çiftdoğrusal form bir (0, 2)-tensör ile aynı şeydir;(0, 2)-tensörünün bir örneği bir iç çarpım'dır, ama iç çarpımları (0, 2)-tensörlerinin hepsi değildir. (0, M)-tablosunun girişi içinde, M temel vektörü boşluk veya manifoldu boyutu gösterir.

n, m	n = 0	n = 1	n = 2	...	n = N	...
m = 0	Skaler, örneğin skaler eğrilik	vektör örneğin yön vektörü)	çift-vektör,örneğin ters metrik tensör		N-vektör, N-bıçakların bir toplamı
m = 1	kovektör, doğrusal fonksiyonel, 1-form (örneğin bir skaler alanın eğimi)	Doğrusal dönüşüm,Kronecker delta
m = 2	çift doğrusal form,örneğin iç çarpım, Metrik tensör, Ricci eğriliği, 2-form, simplektik formu	örneğin üç boyutta dış çarpım	örneğin elastisite tensörü
m = 3	örneğin 3-form	örneğin Riemann eğriliği tensörü
...
m = M	örneğin M-form örneğin hacim formu
...

Bir indis yükseltilerek bir (n, m)-tensör bir (n + 1, m − 1)-tensör üretilebilir; tabloya çapraz yukarı ve sağa hareket olarak görüntülenebilir. Simetriklik, bir dizin indirme çapraz aşağı hareket olarak görüntülenebilir ve tabloda sola olabilir.Bir (n, m)-tensorünün ürünü bir (n − 1, m − 1)-tensörünün bir üst ile bir alt indisi büzülmedir;Bu tabloda çapraz yukarı ve sola hareket olarak görüntülenebilir.

Gösterim

Ricci hesabı

Ricci hesabı modern şekilcilik ve tensor indisi için gösterimdir:iç ve dış çarpımlar ayrıştırılır, kovaryans ve kontravaryanslar, tensor bileşenlerinin toplam'ları, simetri ve antisimetri ve kısmi ve kovaryans türevler.

Einstein Toplam kuralı

Einstein Toplam kuralı kapalı toplamını bırakıp dağıtarak toplama işaretleri ile yazılır,. Herhangi tekrarlanan indis sembol üzerinde toplanır: bir tensör ifade eden indis i belirli bir dönem içinde iki kez kullanılırsa, bu terim tüm i için özetlenebilir olduğu anlamına gelir.. indislerin birkaç farklı çiftleri bu şekilde özetlenebilir.

Penrose grafiksel gösterimi

Penrose grafiksel gösterimi is şekiller ile tensörler için sembollerin yerini şematik bir gösterimdir, ve doğrular ve eğriler yardımıyla indisleri. Bu taban ögelerin bağımsız olmasını ve indisleri için sembolleri gerektirir.

Soyut indis gösterimi

Soyut indis gösterimi is indisleri bundan böyle olarak sayısal düşünülen şekilde tensörler yazmak için bir yol, ama daha çok belirsizdir. Bu gösterim indis bağımsız gösteriminin taban-bağımsızlığını ve indislerin anlamlılığını ele verir.

Bileşen-bağımsız gösterimde

A Tensörlerin bileşen bağımsız çalışması tensör gösteriminin herhangi baza ihtiyaç duymadan kullanılacağını vurguluyor ve vektör uzaylarının tensör çarpımı terimlerimin içindeki tanımdır.

Ayrıca bakınız

Temel

• Kartezyen tensör
• Lif demeti
• Tensör teorisinin dili
• Çokludoğrusal izdüşüm
• Tek-form
• Modüllerin tensör çarpımları

Uygulamalar

• Teknolojide tensör teorisinin uygulamaları
• Kovaryant türev
• Eğrilik
• Difüzyon tensör MRI
• Einstein alan denklemleri
• Akışkanlar mekaniği
• Çokludoğrusal altuzay öğrenimi
• Riemannian geometrisi
• Yapısal Tensör
• Tensör bozulması
• Tensör türevleri
• Tensör yazılımı

Kaynakça

Genel

Özel

Bu makale, Creative Commons Attribution/Share-Alike License altında lisanslanan PlanetMath'deki {{{title}}} materyalini içermektedir.

Dış bağlantılar

• Eric W. Weisstein, Tensör (MathWorld)
• Introduction to Vectors and Tensors, Vol 1: Linear and Multilinear Algebra10 Mayıs 2010 tarihinde Wayback Machine sitesinde arşivlendi. by Ray M. Bowen and C. C. Wang.
• Introduction to Vectors and Tensors, Vol 2: Vector and Tensor Analysis10 Mayıs 2010 tarihinde Wayback Machine sitesinde arşivlendi. by Ray M. Bowen and C. C. Wang.
• An Introduction to Tensors for Students of Physics and Engineering26 Haziran 2010 tarihinde Wayback Machine sitesinde arşivlendi. by Joseph C. Kolecki, released by NASA
• A discussion of the various approaches to teaching tensors, and recommendations of textbooks
• Introduction to tensors8 Aralık 2013 tarihinde Wayback Machine sitesinde arşivlendi. an original approach by S Poirier
• A Quick Introduction to Tensor Analysis23 Haziran 2014 tarihinde Wayback Machine sitesinde arşivlendi. by R. A. Sharipov.