Birim hiperbol

birim hiperbolü mavi, eşleniği yeşil, ve asimptotu kırmızı renktedir.

Geometride, Kartezyen düzleminde $x^{2}-y^{2}=1.$ formülünü sağlayan (x,y) noktalar kümesine birim hiperbol denir. Belirsiz dikey gruplar çalışmasında, birim hiperbol bir alternatif radial uzunluk için bir temel oluşturur.

$r={\sqrt {x^{2}-y^{2}}}.$

Oysa birim çember merkezini çevreleyen,düzlemde bunu tamamlayacak konjuge hiperbolü$y^{2}-x^{2}=1$ birim hiperbol gerektirir. Hiperbol çiftleri asimptotları y = x ve y = −x olarak paylaşır. Birim hiperbolün eşleniği kullanıldığında alternatif radyal uzunluk ; $r={\sqrt {y^{2}-x^{2}}}.$ Birim hiperbol yönelimi, ölçeği ve konumuyla dikdörtgen hiperbolünün özel bir durumudur. Aslında, aykırılığı ${\sqrt {2}}.$’ ye eşittir. Birim hiperbol analitik geometri amacıyla yer değiştirmiş olan çember gibi farklı uygulamalarda bulunabilir. Göze çarpan bir örnek de sözde Öklid uzayı olarak,uzay zamanının tasviridir. Birim hiperbolün asimptotları bir ışık konisi oluştururlar. Ayrıca, Gregoire de Saint-Vincent tarafından yönetilen hiperbolik sektörler alanına dikkat etmek gerekirse, bu alanlarda modern parametrelere ve logaritma fonksiyonuna yol açar. Eşlenik hiperbollerin ve hiperbolik açıların kavramları anlaşıldığı zaman, birim çemberin etrafına kurulan klasik karmaşık sayılar, birim hiperbol etrafında numaraları değiştirilebilir.

Asimptotlar

Genel olarak asimptot çizgileri bir eğriye doğru birleştiği söylenebilir. Cebirsel geometride ve cebirsel eğriler teorisinde asimptot için farklı bir yaklaşım vardır. Eğri ilk olarak homojen koordinatlar kullanılarak projektif düzlemi yorumlar. Sonra, asimptotlar sonsuzda bir noktada tanjantın izdüşüm eğrisi olur. Bu nedenle, yakınsama ve kavram mesafesini yakalamaya ihtiyaç duyulmaz. Bilinen bir sistem olan (x, y, z) sonsuz doğrultusunda z=0 denklemi tarafından karar verilen homojen koordinatlardır. Örneğin ; C.G.GİBSON’ın yazdığına göre ;

Standart dikdörtgen hiperbolü için $\scriptstyle f=x^{2}-y^{2}-1$ve R² de izdüşüm eğrisine karşılık gelen fonksiyon; F = x^2 - y^2 - z^2’dur. Z =0 noktalarında P = (1 : 1 : 0) ve Q = (1 : −1 : 0).

Minkowski diyagramı

Minkowski diyagramı uzamsal yönü tek bir boyutta kısıtlı olan bir uzay düzleminde çizilir.

• 30 cm uzunluğunda ve birimleri nanosaniye veya
• Astronomik birim ve 8dk 20saniye veya aralıklı
• Işık yılı ve yıllar

Koordinat ölçeklerinin her biri foton olaylarının bağlantıları boyunca eğimin artı ve eksi köşegenleri ile sonuçlanır. Hermann Minkowski diyagramını, görelelik dönüşümlerini tanımlamak için beş element oluşturur; birim hiperbol, onun eşlenik hiperbolü, hiperbolün eksenleri,birim hiperbolün esneklik çapı.Referans çerçevesi eksenleri ile düzlem bir dinlenme anlamına gelir. Bir hiperbolün eni hızlı bir hareket içinde bir referans çerçevesini temsil eder. a; tanh a = y/x ve (x,y) birim hiperbol üzerindeki son noktanın çapını verir. Eşleniğin çapı hızlı a’ya tekabül eden eşzamanlı mekânsal alt düzlemi temsil eder. Bu makalede birim hiperbolü bir kalibrasyon hiperbolüdür. Yaygın olarak, görecelik çalışmasında dikey ekseni ile hiperbol birincil olarak hesaplanır:

zamanın ok işareti figürün altından üstüne doğru gider-Richard Feynman tarafından bir kongrede kabul edilen Feynman’ın ünlü diyagramlarıdır. Boşluk zaman ekseni dik düzlemler tarafından temsil edilmektedir. Ortada eşsiz bir durum bulunmaktadır.

Parametreleştirme

birim hiperbol dalları &alpha’ ya bağlı noktalarında (cosh α, sinh α) ve (−cosh α, −sinh α) hiperbolik açı parametresi

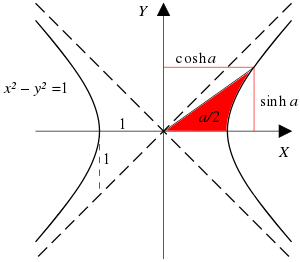
Birim hiperbolü parametreleştirmek için bir yol hiperbol ile başlar,xy = 1 ile parametrelendirilen üstel fonksiyonu ;

$(e^{t},\ e^{-t}).$

Bu hiperbol, matrıxe sahip doğrusal bir eşleşme tarafından birim hiperbole dönüşür. $A={\tfrac {1}{2}}{\begin{pmatrix}1&1\\1&-1\end{pmatrix}}\ :$

$(e^{t},\ e^{-t})\ A=({\frac {e^{t}+e^{-t}}{2}},\ {\frac {e^{t}-e^{-t}}{2}})=(\cosh t,\ \sinh t).$

t olan bu parametre hiperbolik açıdır ve bu hiperbolik fonksiyonun tanımıdır. Dinamiğin elementlerinde birim hiperbolün parametreleştirilmesinin erken bir tanımı vardır W.K. Clifford tarafından 1878 de ortaya atılmıştır. Clifford bir hiperbolde yarı harmonik hareketi aşağıdaki bilgilerle açıklar; Eliptik harmonik harekete :The motion $\rho =\alpha \cosh(nt+\epsilon )+\beta \sinh(nt+\epsilon )$ bazı benzetmeler vardır… İvme ${\ddot {\rho }}=n^{2}\rho \ ;$  bu nedenle, merkezden uzaklığı genellikle orantılıdır ama yönettiği merkezinden uzaktadır. Belirli bir koni olarak,hiperbol bir koninin ek noktaları tarafından parametreleştirilmiş olabilir. Aşağıdaki tanımlar Rus analistler tarafından verilmiştir. Koni üzerinde tespit edilen sabit bir E noktası. E ye doğru çizilen düz bir çizgi üzerinde bir nokta düşünün koninin kesişimleri AB olan,ikinci kez kesişen A ve B noktalarının toplamıdır. Hiperbol için x^2 - y^2 = 1</math> sabit noktası E = (1,0) noktalarının toplamı $(x_{1},\ y_{1})$ ve $(x_{2},\ y_{2})$ nokta $(x_{1}x_{2}+y_{1}y_{2},\ y_{1}x_{2}+y_{2}x_{1})$ parametrelerinin altında $x=\cosh \ t$ ve $y=\sinh \ t$ bu eklenme parametre t ‘nin eklenmesinden gelir.

Karmaşık düzlem cebir

Mademki birim çember karmaşık sayılarla ilişkili, birim çember ise j ² = +1 olduğu yerde z = x + y j yi içeren ayrık karmaşık sayı düzleminin bir anahtarıdır. j’nin düzlem üzerindeki hareketini koordinatlar arasında değiş tokuş edebilmesi için, jz = y + x j bu formülü kullanabiliriz. Özellikle, bu hareket eşleniği ve birim hiperbol arasında karşılıklı değiş tokuş yapar ve ayrıca hiperbollerin eşlenik çaplarının çiftleri arasında karşılıklı değiş tokuş olur. Hiperbolik açı parametresi a,noktaların içerdiği birim hiperbol

$\pm (\cosh a+j\sinh a)$ j = (0,1) olduğunda.

Birim hiperbolün sağ kolu pozitif tam sayıya karşılık gelir. Aslında bu kol j ekseninde rol oynayan üstel eşin bir resmidir. Bu yüzden ;

$\exp(aj)exp(bj)=\exp((a+b)j),$

Bu kol çarpmanın altında bir koldur. Çember grubunun aksine, bu birim hiperbol grubu sıkı ve etkin değildir .Sıradan karmaşık düzlemlere benzer olarak bir nokta köşegenler üzerinde değildir, hiperbolün parametreleştirilmesinin ve alternatif radyal uzunluğun kullanıldığı polar bir ayrışmaya sahiptir.

Kaynakça

• F. Reese Harvey (1990) Spinors and calibrations, Figure 4.33, page 70, Academic Press, ISBN 0-12-329650-1 .