Ağ modeli
Ağ modeli yöneylem araştırmasında belirlenmiş bir sıra problemin düğümler ve dal veya bağlantilardan oluşan bir şebeke halinde tanımlanıp modellemesi türü olup ve tanımlanan sebeke problemlerinin çözümlenmesi için ortaya çıkartılan özel şebeke problemi algoritmalardan oluşur. Bu türlü çalışmalarda önce problemin ögeleri ve amacı tarif edilir. Sonra problemin şekil olarak veya matris olarak dallar ile birbirlerine bağlı düğümler halinde yapılandırılıp tanımlanması gerekir. Örneğin problem bir şehre kurulacak su borusu şebekesinin, bütün şehre en ucuz maliyet ile nasıl kurulacağıdir. Bu problem bir mümkün olan bütün bağlantı parçalarını, maliyetleri ve kapasiteleri gösteren şebeke halinde ifade edilir. Bu problem ve yapılanan model bir minimum maliyet kapasiteli sebeke problemi olduğu için bu çeşit model problemi çözmek için geliştirilmiş olan özel algoritmalardan birini kullanarak çözülebilir.
En çok kullanilan ve iyi geliştirilmiş özel şebeke modeli algoritması bulunan problemler arasında şunlar bulunur:
- Minimum kapsayan ağaç problemleri ve algoritmaları;
- En kısa yol problemi ve algoritmaları;
- Maksimum akış problemi ve algoritmaları;
- Minimum maliyet kapasiteli şebeke problemleri ve algoritmaları;
- Nakliyat problemi ve algoritmaları;
- Kritik yol problemleri ve algoritmaları
Bu şebeke problemlerini birçogu, özel şebeke modeli algoritmaları yanında, ayrıca programlama (doğrusal programlama, tamsayıli programlama, dinamik programlama) problemi olarak da formüle edilip çözülebilirler.
Şebeke Tanımları[değiştir | kaynağı değiştir]
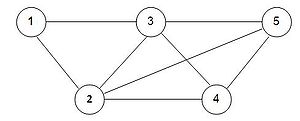
Bir şebeke birbirlerine dallar (veya bağlantılar) ile bağlanmış bir dizi düğümden oluşur. Matematik konvansiyanuna gore, bir şebeke (N, A) notasyonuyla ifade edilir. Buradaki N, düğümler kümesi, A ise bağlantılar kümesidir. Örneğin şekildeki şebeke aşağıdaki gibi tanımlanır:
N = {1, 2, 3, 4, 5}
A = {(1, 3), (1, 2), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)}