Tetrasyon

$(e^{-1})^e \le x \le e^{e^{-1}})$ tabanları için $\lim_{n\rightarrow \infty} x^{\frac{n}{}}$ sonsuz üslü kulesi

Matematikte, tetrasyon (hiper-4 olarak ta bilinir), üslü sayıdan sonra gelen ilk aşırı işlecin tekrarlı üssüdür. Tetrasyonun İngilizce karşılığı olan tetration kelimesi ilk kez matematikçi Reuben Louis Goodstein tarafından, tetra- (dört) ve iteration (tekrar)dan türetilerek kullanılmaya başlandı. Tetrasyon çok büyük sayıların gösterimi için kullanıldı. Fakat birkaç pratik uygulaması vardır. Bu yüzden sadece saf matematik incelenir. Burada aşırı işlecin ilk dört örneğin gösteriliyor. Tekrasyon dördüncüsüdür:

1. toplama

   Normal bilinen toplama işlemi.

2. çarpma

   $a \times n = \underbrace{a + a + \cdots + a}_n$

   genellikle temel işlemlerden birini ifade eder. Fakat doğal sayılar gibi özel durumlar için kendine n kere eklenen a olabilir.

3. üs alma

   $a^n = \underbrace{a \times a \times \cdots \times a}_n$

   a nın kendisi ile n kere çarpılması.

4. tetrasyon

   ${^{n}a} = \underbrace{a^{a^{\cdot^{\cdot^{a}}}}}_n$

   a 'nın kendisiyle n kere üssünün alınması.

buradaki herbir işlem, bir öncekinin tekrarı şeklinde tanımlanır. Tetrasyonunu bu işlemlerden ayıran özellik, ilk üçü, (toplama, çarpma ve üs alma) n nin karmaşık değerler ile genelleşmesiyken, tetrasyonun henüz keşfedilen düzenli bir genelleştirilmesi yoktur ve tetrasyon, bir temel fonksiyon olarak nitelendirilmez.

Toplama (a + n), en temel işlemdir. Çarpma (an) da temel fonksiyondur. Tetrasyon ($^{n}a$), n nin a tane kuvvetini içeren bir dizi olarak düşünülebilir. a değişkeni ilerleyen bölümlerde temel değişken olarak adlandırılırken n değişkeni de yükseklik değişkeni olarak adlandırılacak (integral ilk yaklaşımdır, fakat kesirli olarak genelleştirilebilir, gerçel ve karmaşık yükseklik gibi).

Tanım

Her pozitif reel $a > 0$ ve negatif olmayan tam sayı $n \ge 0$ için $\,\! {^{n}a}$ şöyle tanımlanır:

• $\,\! {^{0}a} = 1$ ($n = 0$ ise) ve
• $\,\! {^{n}a} = a^{(^{n-1}a)}$ (eğer $n > 0$ ise)

Tekrarlı kuvvetler

Tanımdan da görüldüğü üzere, tetrasyon "üslü kuvvet" olarak hesaplandığında üs, öncelikle en derin seviyede alınır (gösterimdeki en yüksek derece) Diğer ifadeyle:

$\,\!\ ^{4}2 = 2^{2^{2^2}} = 2^{\left(2^{\left(2^2\right)}\right)} = 2^{\left(2^4\right)} = 2^{16} = 65.\!536$

Üssün birleşme olmadığına dikkat edin. Böylece, diğer sıradaki hesaplama, farklı bir cevaba gider:

$\,\! 2^{2^{2^2}} \ne \left({\left(2^2\right)}^2\right)^2 = 2^{2 \cdot 2 \cdot2} = 256$

Burada, üslü kuvvetler, yukarıdan aşağıya doğru (veya sağdan sola doğru) hesaplanmalıdır.

Terimbilim

Tetrasyon için birçok terim ve herbirinin kullanımı için mantıksal düşünceler vardır. Fakat bazıları, birçok nedenden dolayı yaygınlık kazanamadı. Burada birkaçından bahsedilecektir.

• Tetration (tetrasyon) terimi, 1947'de Goodstein tarafından geliştirildi.
• Superexponentiation (süper üs) terimi Bromer tarafından geliştirildi.
• Hyperpower (aşırı kuvvet), hyper (aşırı) ve power (kuvvet) kelimelerinin birleşimidir ve tetrasyonun uygun şekilde açıklar.
• Power tower (üslü kule), ara sıra kullanılır. Örneğin, ${\ \atop {\ }} {{\underbrace{a^{a^{\cdot^{\cdot^{a}}}}}} \atop n}$ " n sırasının üslü kulesi"

Tetrasyon birbirine yakın ilişkiye sahip fonksiyon ve ifadelerle genellikle karıştırılıyor. Bundan dolayıdır ki tetrasyon ile ilgili birçok terim kullanılıyor. Burada birkaçını vereceğiz:

Form	Terimbilimi
$a^{a^{\cdot^{\cdot^{a^a}}}}$	Tetrasyon
$a^{a^{\cdot^{\cdot^{a^x}}}}$	Tekrarlı üsler
$a_1^{a_2^{\cdot^{\cdot^{a_n}}}}$	İçiçe üsler (kuleler)
$a_1^{a_2^{a_3^{\cdot^{\cdot^\cdot}}}}$	Sonsuz üsler (kuleler)

İlk iki ifadede a, tabandır. Kez (kere) sayısı olan diğer a, yükseklikdir. Üçüncü ifadede n, yüksekliktir, fakat herbirinin tabanı farklıdır.

Gösterim

Tetrasyonun yazılabileceği gösterimler şunlardır:

Ad	Form	Açıklama
Standart gösterim	$\,{}^{n}a$	Maurer [1901] ve Goodstein [1947] tarafından kullanıldı; Rudy Rucker kitabı olan Sonsuzluk ve zihin, bu gösterimi popüler yaptı.
Knuth yukarı ok gösterimi	$a {\uparrow\uparrow} n$	Daha fazla oklar koyarak genişlemeyi veya daha güçlü olmayı sağlar.
Conway dizisi ok gösterimi	$a \rightarrow n \rightarrow 2$	2 sayısının artırarak genişlemeyi sağlar (yukarıdakinin genişlemesiyle eşdeğerdir). Ayrıca, dizi genişletilerek daha da güçlenir.
Ackermann işlevi	${}^{n}2 = \operatorname{A}(4, n - 3) + 3$	Ackermann işlevinin $a=2$ için yazılan özel durumudur.
Tekrarlı üstel gösterimi	${}^{n}a = \exp_a^n(1)$	1'den farklı başlangıç değerlerine sahip olan tekrarlı üstellerin basit genişlemesini sağlar.
Hooshmand gösterimi	$\operatorname{uxp}_a n, \, a^{\frac{n}{}}$
Aşırı işleç gösterimi	$a^{(4)}n, \, \operatorname{hiper}_4(a,n)$	4 sayısını arttırarak genişleme sağlar. Bu aşırı işleçlerin ailesini oluşturur
ASCII gösterimi	a^^n	Yukarı ok, düzeltme işareti (^) ile aynı kullanıldığında, tetrasyon işleci de (^^) olarak yazılır.

Yukarıdaki gösterimlerden biri, tekrarlı üstel gösterimi kullanır. Bu genellikle şöyle tanımlanır:

$\exp_a^n(x) = a^{a^{\cdot^{\cdot^{a^x}}}}$ n tane "a".

Tekrarlı üsler için çok fazla gösterim yoktur. Fakat birkaçını verelim:

Ad	Form	Açıklama
Standart gösterim	$\exp_a^n(x)$	Euler dizi gösterimi $\exp_a(x) = a^x$, ve tekrar gösterimi $f^n(x)$.
Knuth yukarı ok gösterimi	$(a{\uparrow})^n(x)$	Okların sayısını arttırarak süper kuvvetler ve süper üslü fonksiyonları sağlar. Bu gösterim büyük sayılarda kullanılır.
Ioannis Galidakis gösterimi	$\,{}^{n}(a, x)$	Büyük ifadelerin temelini oluşturun.
ASCII (yardımcı)	a^^n@x	Tekrarlı üstelin görünüm temeli yardımcı tetrasyondur.
ASCII (standart)	exp_a^n(x)	Standart gösterimin temelidir.

Örnekler

Aşağıdaki tablodaki çoğu değerler, bilimsel gösterimde yazmak çok zordur. Bundan dolayı tekrarlı üstel gösterim onları 10 tabanında ifade etti. Değerlerdeki ondalık nokta yaklaşıktır.

$x$	${}^{2}x$	${}^{3}x$	${}^{4}x$
1	1	1	1
2	4	16	65.536
3	27	7.625.597.484.987	$\exp_{10}^3(1,09902)$
4	256	$\exp_{10}^2(2,18788)$	$\exp_{10}^3(2,18726)$
5	3.125	$\exp_{10}^2(3,33931)$	$\exp_{10}^3(3,33928)$
6	46.656	$\exp_{10}^2(4,55997)$	$\exp_{10}^3(4,55997)$
7	823.543	$\exp_{10}^2(5,84259)$	$\exp_{10}^3(5,84259)$
8	16.777.216	$\exp_{10}^2(7,18045)$	$\exp_{10}^3(7,18045)$
9	387.420.489	$\exp_{10}^2(8,56784)$	$\exp_{10}^3(8,56784)$
10	10.000.000.000	$\exp_{10}^3(1)$	$\exp_{10}^4(1)$

Çok ilkel fonksiyonlardaki yaklaşımlar

Polinom yaklaşımları

Lineer yaklaşım

Lineer yaklaşımı (süreklilik isteğinin çözümüe, differensiyellenebilirlik yaklaşımı) şöyle elde edilir:

${}^{x}a \approx \begin{cases} \log_a({}^{(x+1)}a) & x \le -1 \mbox{ için} \\ 1 + x & -1 < x \le 0 \mbox{ için} \\ a^{\left({}^{(x-1)}a\right)} & x > 0 \mbox{ için} \end{cases}$

Bundan dolayı:

Yaklaşım	Tanım kümesi
$\,{}^{x}a \approx x+1$	$-1<x<0$ için
$\,{}^{x}a \approx a^x$	$0<x<1$ için
$\,{}^{x}a \approx a^{a^{(x-1)}}$	$1<x<2$ için

ve böylece devam eder.

Örnekler: $\,{}^{(\pi / 2)}e \approx 5,868...,\; {}^{-4,3}0,5 \approx 4,03335...,\;$

Ana teorem Hooshmand'e göre: $0 <a \neq 1$'dir. Eğer $f:(-2,+\infty)\rightarrow \mathbb{R}$, istenmeyen durumlara doğru giderse:

• $f(x)=a^{f(x-1)} \; \; \mbox{ tüm} \; \; x>-1 \mbox{ ve} \; f(0)=1 \mbox{ için},$
• $f$, $(-1,0)$'de türevlenebilir,
• $f^\prime$ fonksiyonu, $(-1,0)$'da azalmayan veya artmayan bir fonksiyondur,
• $f^\prime (0^+) = (\ln a) f^\prime (0^-) \mbox{ veya } f^\prime (-1^+) = f^\prime (0^-).$

Daha sonra $f$, şu denklemle benzersiz tanımlanır:

$\; \; \; f(x)=\exp^{[x]}_a (a^{(x)})=\exp^{[x+1]}_a((x)) \; \; \; \mbox{tüm} \; \; x>-2 \mbox{ için }.$

Buradaki $(x)=x-[x]$, x in kısmi parçasını ifade eder ve $\exp^{[x]}_a$ fonksiyonu, $\exp_a$ fonksiyonunun $[x]$-tekrarlı fonksiyonudur.

İkinci ve dördüncü şartlar ispattır.

${}^xe$ doğal tetrasyon fonksiyonundaki lineer yaklaşımı sürekli olarak türevlenebilir. Fakat ikinci türevi, argümanının tam sayısında bulunmaz. Hooshmand, onun için de söyle bir eşsiz teorem türetti:

Eğer $f: (-2, +\infty)\rightarrow \mathbb{R}$ ise, sürekli fonksiyon şöyledir:

• $f(x)=e^{f(x-1)} \; \; \mbox{tüm} \; \; x>-1, \; f(0)=1$ için,
• $f$, $(-1,0)$'de yakınsar,
• $f^\prime (0^-)\leq f^\prime (0^+).$

Sonra $f=\mbox{uxp}$ olur.

Buradaki ispat bir öncekine çok benzer. Özyineleme eşitliği, $f^\prime (-1^+) = f^\prime (0^+),$ olduğunu sağlar ve yakınsaklık şartı (-1, 0)'de $f$ fonksiyonunun lineer olduğunu ifade eder.

Bundan dolayı doğal tetrasyondaki lineer yaklaşımı, sadece $f(x)=e^{f(x-1)} \; \; (x>-1)$ eşitliğinin çözümüdür ve $f(0)=1$, $(-1,+\infty)$'de yakınsaktır. Diğer tüm uygun türevlenebilir çözümlerin (-1, 0) aralığında bir büküm noktası olması gerekir.

Yüksek sıralı yaklaşımlar

İkinci dereceden yaklaşım şöyledir:

${}^{x}a \approx \begin{cases} \log_a({}^{(x+1)}a) & x \le -1 \mbox{ için } \\ 1 + \frac{2\log(a)}{1+\log(a)}x - \frac{1-\log(a)}{1+\log(a)}x^2 & -1 < x \le 0 \mbox{ için } \\ a^{\left({}^{(x-1)}a\right)} & x > 0 \mbox{ için } \end{cases}$

Bu ifade tüm $x > 0$ için türevlenebilir. Faka iki kez türevlenemez. Eğer $a = e$ ise bu, lineer yaklaşım gibidir.

Genişlemeler

Tetrasyon, ${^n 0}$ ve diğer tanım kümelerini ifade etmek için genişletilebilir.

Tabanlarda tanım kümesi genişlemesi

Sıfır tabanında genişleme

$0^0$ üs ifadesi sürekli olarak tanımlanmaz. $\,{^{n}0}$ tetrasyonu da, daha önceki formüle göre iyi tanımlanmaz. Yine de $\lim_{x\rightarrow0} {}^{n}x$ şöyle tanımlanabilir:

$\lim_{x\rightarrow0} {}^{n}x = \begin{cases} 1, & n \mbox{ çift} \\ 0, & n \mbox{ tek} \end{cases}$

Buradan ${}^{n}0 = \lim_{x\rightarrow0} {}^{n}x$ ifadesini sürekli tanımlayabiliriz. Bu $0^0 = 1$ tanımının eşdeğeridir.

Bu genişleme altında, ${}^{0}0 = 1$. Böylece asıl tanım koruyarak ${^{0}a} = 1$ kuralı sağlanır.

Karmaşık tabanlarda genişleme

Periyoda göre tetrasyon

Sızıntıya göre tetrasyon

Karmaşık sayılar kuvvetlerle arttarken, tetrasyon, $z = a + bi$ formunun tabanlarında uygulanabilir. Buradaki $i$, -1'in kareköküdür. Örneğin, ${}^{n}z$ ($z=i$) tetrasyonu, doğal logaritma prensibi kullanılarak ifade edilebilir. Euler formülünü kullanarak şöyle bir ilişki elde edebiliriz:

$i^{a+bi} = e^{{i\pi \over 2} (a+bi)} = e^{-{b\pi \over 2}} \left(\cos{a\pi \over 2} + i \sin{a\pi \over 2}\right)$

Bu, ${}^{(n+1)}i = a'+b'i$ için tekrarlı bir tanım ortaya çıkartır. Her ${}^{n}i = a+bi$ için:

$a' = e^{-{b\pi \over 2}} \cos{a\pi \over 2}$

$b' = e^{-{b\pi \over 2}} \sin{a\pi \over 2}$

Aşağıdaki yaklaşım değerleri türetilebilir:

${}^{n}i$	Yaklaşım Değeri
${}^{1}i = i$	i
${}^{2}i = i^{\left({}^{1}i\right)}$	$0,2079$
${}^{3}i = i^{\left({}^{2}i\right)}$	$0,9472 + 0,3208i$
${}^{4}i = i^{\left({}^{3}i\right)}$	$0,0501 + 0,6021i$
${}^{5}i = i^{\left({}^{4}i\right)}$	$0,3872 + 0,0305i$
${}^{6}i = i^{\left({}^{5}i\right)}$	$0,7823 + 0,5446i$
${}^{7}i = i^{\left({}^{6}i\right)}$	$0,1426 + 0,4005i$
${}^{8}i = i^{\left({}^{7}i\right)}$	$0,5198 + 0,1184i$
${}^{9}i = i^{\left({}^{8}i\right)}$	$0,5686 + 0,6051i$

Önceki bölümle ters ilişkiyi çözme, n nin negatif değerli beklenen $\,{}^{0}i = 1$ ve $\,{}^{(-1)}i = 0$'ı sağlar. Bunun için sanal eksene sonsuz sonuç verilir.

(Tekrarlı) "yükseklikler" için tanım kümesi genişlemeleri

Sonsuz yükseklik genişlemesi

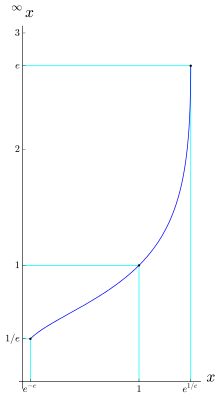
Tetrasyon sonsuz yüksekliklere genişletilebilir (${}^{n}a$'deki n). Örneğin, $\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdot^{\cdot^{\cdot}}}}}$ ifadesi 2'ye yakınsar, bundan dolayı "2'ye eşittir" denir. 2'ye doğru gidiş, küçük sonlu kuleyi hesaplayarak görülebilir:

$\begin{align} \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{1,41}}}}} &= \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{1,63}}}} \\ &= \sqrt{2}^{\sqrt{2}^{\sqrt{2}^{1,76}}} = \sqrt{2}^{\sqrt{2}^{1,84}} \\ &= \sqrt{2}^{1,89} = 1,93 \end{align}$

Genellikle $x^{x^{\cdot^{\cdot^{\cdot}}}}$ sonsuz kuvvet kulesi, ${}^{n}x$'in limiti (sınırı) olarak tanımlanır. Burada n e^−e ≤ x ≤ e^1/e için sonsuzluğa gider.

Negatif yüksekliklere (sınırlı) genişleme

Asıl kuralı korumak için:

${^{(k+1)}a} = a^{({^{k}a})}$

$k$'nın negatif değerleri için, özyineleme ilişkisini kullanmalıyız:

${^{k}a} = \log_a \left( {^{(k+1)}a} \right)$

Buradan:

${}^{(-1)}a = \log_{a} \left( {}^{0}a \right) = \log_{a} 1 = 0$

Bununla beraber daha küçük negatif değerler, bu yolla iyi tanım verme. Çünkü,

${}^{(-2)}a = \log_{a} \left( {}^{-1}a \right) = \log_{a} 0$

iyi tanımlı değildir.

$\,\! {^{(-1)}1}$'in her tanımı $n = 1$ için kuralla uyumlu olduğuna dikkat edin. Çünkü

her $\,\! n = {^{(-1)}1}$ için, ${^{0}1} = 1 = 1^n$'dir.

Gerçek yüksekliklere genişleme

Burada, genişleme tetrasyonunun genel problemlerinin çözümü için $n$'nin reel veya karmaşık değerlerinde, yaygın olarak kullanılan kabul edilmiş bir çözüm yoktur. Çeşitli yaklaşımlar aşağıdaki gösteriliyor.

Genelde problem, a > 0 ve, $x > -2$ değerleri için $\,f(x) = {}^{x}a$ gibi bir süper üstel fonksiyon bulunuyor ki buda yeterince tatminkârdır.

• $\,{}^{(-1)}a = 0$
• $\,{}^{0}a = 1$
• $\,{}^{x}a = a^{\left({}^{(x-1)}a\right)}$ tüm reel x > -1 için.
• Dördüncü koşul genellikle şunlardan biridir:

• Bir süreklilik koşulu (genellikle sadece ${}^{x}a$, her iki değişken için $x > 0$ şartılya süreklidir).
• Bir türevlenebilirlik koşulu (x 'de bir kez, iki kez, k kez veya sonsuz kez türevlenebilir).
• Bir uygunluk şartı (x 'de iki kez türevlenebilirliği ifade eder) şöyledir:

$\left( \frac{d^2}{dx^2}f(x) > 0\right)$ tüm $x > 0$ için

Dördüncü koşul kişiden kişiye ve yaklaşımlara göre değişirr. Tetrasyonunu gerçel yüksekliklere genişletmek için iki ana yaklaşım vardır. Birincisi uygunluk koşulu, diğeri de türevlenebilirlik koşuludur. Bu iki yaklaşım, birbirleriyle tutarsız sonuçlar üretmesi, onların çok farklı olduğunu gösterdi.

Neyse ki, bir uzunluğun içindekilerden biri, tüm pozitif reel sayılar için genişletilebilir. Bir içsel uzunluk için $\,{}^{x}a$ tanımlıysa, tam fonksiyon tüm $x > -2$ için geçerlidir.

Karmaşık yüksekliklere genişleme

$f=F(x+{\rm i}y)$ tetrasyonunun karmaşık düzlemde analitik genişlemesinin çizimi. $|f|=1,e^{\pm 1},e^{\pm 2},\ldots$ ve $\arg(f)=0,\pm 1,\pm 2,\ldots$ dereceleri kalın eğimlerle gösteriliyor.

Şöyle bir konjektür vardır: F(z+1)=exp(F(z)) eşitliğinin çözümü için eşsiz bir F fonksiyonu vardır ve ek F(0)=1 ve F(z) yaklaşımlarını sağlar. Bu fonksiyon sağdaki şekilde görülüyor.

Ters fonksiyonlar

Tetrasyonun Ters fonksiyonları genellikle süper kök ve süper logaritma olarak adlandırılır. $x^x$'in süper kökün karesi olan $\mathrm{ssrt}(x)$, Lambert W fonksiyonu ile şöyle ifade edilebilir:

$\mathrm{ssqrt}(x)=e^{W(\mathrm{ln}(x))}=\frac{\mathrm{ln}(x)}{W(\mathrm{ln}(x))}$

Her n > tamsayıları için ⁿx şeklinde fonksiyon vardır ve bu fonksiyon x ≥ için artarak 1=ⁿ1 = eşitliği elde edilir. Böylece x in n. süper kökü x ≥ 1 için elde edilir.

Yine de, eğer yukarıdaki lineer yaklaşım kullanılır ve -1≤y≤0 şart sağlanırsa, 1= ^yx = y + 1 olur. Böylece 1=^ysroot(y + 1) elde edilemez.

slog_a x süper algoritması, tüm gerçel x ve a > 1 sayıları için geçerlidir.

$\mathrm{slog}_a$ fonksiyonu:

$\mathrm{slog}_a {^x a} = x$

$\mathrm{slog}_a a^x = 1 + \mathrm{slog}_a x$

$\mathrm{slog}_a x = 1 + \mathrm{slog}_a \log_a x$

$\mathrm{slog}_a x > -2$

İnfra logaritma fonksiyonu, ultra üstel fonksiyonun iki katıdır ve $\mathrm{iog}_a$ şeklinde ifade edilir. Eğer $a>1$ ise $\mathrm{uxp}_a$ fonksiyonunun tersi olur.

Süper kök

Süper kök, tetrasyonun iki ters fonksiyonundan biridir. Sadece, kökler ve logaritma üstel olarak iki ters fonksiyonken, keza tetrasyonunda iki ters fonksiyonu vardır: süper kök ve süper logaritma. Süper kök, tetrasyonun tabanını ifade eden ters fonksiyonudur: eğer $^n y = x$ ise y de x in n. süper kökü olur. Örneğin;

$^4 2 = 2^{2^{2^{2}}} = 65.536$

böylece 2, 65.536'nın 4. köküdür ve

$^3 3 = 3^{3^{3}} = 7.625.597.484.987$ olur.

Böylece 3, 7.625.597.484.987'nin 3. süper kökü (veya süper küpü)dür.

Süper kökün birkaç pratik uygulaması vardır. Bunlar sadece saf matematikte çalışılır.

Kare kök

2. sıra süper kök veya "süper kare kök" is noteworthy for its simple expression in terms of Lambert W fonksiyonunda terimlerinin basit ifadesi için önemlidir. İfadesi;

$\sqrt{x}_s = e^{W(\ln{x})}$ buradaki $\sqrt{x}_s$, $x$'in süper kare köküdür.

Fonksiyon her ne kadar süper karenin karşıtı olarak tanımlanmış olsa bile, sonsuz üstelin de karşıtıdır. Sonsuz n.kökte şöyledir;

$\sqrt{x}_s = \sqrt[\sqrt[\sqrt[\sqrt[...]{x}]{x}]{x}]{x}.$

Kare kök örnekleri

Aşağıdaki tablo ilk 27 tam sayının süper kare köklerini gösteriyor.

${x}$	$\sqrt{x}_s$	${x}$	$\sqrt{x}_s$	${x}$	$\sqrt{x}_s$
1	1	10	2,506184...	19	2,830223...
2	1,559610...	11	2,555604...	20	2,855308...
3	1,825455...	12	2,600295...	21	2,879069...
4	2	13	2,641061...	22	2,901637...
5	2,129372...	14	2,678523...	23	2,923122...
6	2,231828...	15	2,713163...	24	2,943621...
7	2,316454...	16	2,745368...	25	2,963219...
8	2,388423...	17	2,775449...	26	2,981990...
9	2,450953...	18	2,803663...	27	3

Eğer bir sayının süper kare kökü tam sayı değilse, o irrasyoneldirl. Fakat bunula ilgili herhangi bir ispat ybilinmiyor

Diğer süper kökler

Diğer süper kökler, normal kökle kullanılan aynı tabanda ifade edilebilir: süper küp kökler, $x = y^{y^y}$ olduğunda y üreten fonksiyon, $\sqrt[3]{x}_s$ olarak ifade edilebilir. 4. süper kök, $\sqrt[4]{x}_s$ olarak ifade edilebilir ve bundan dolayı, n^. süper kök, $\sqrt[n]{x}_s$'dir denilebilir.

Süper logaritma

Tetrasyonun iki ters fonksiyonundan biridir. Sadece, kökler ve logaritma üstel olarak iki ters fonksiyonken, keza tetrasyonunda iki ters fonksiyonu vardır: süper logaritma ve süper kök. Süper logaritmayı açıklayan birkaç yol vardır:

• Üstel fonksiyonların Abel fonksiyonu olarak,
• Tetrasyonun yüksekliğini ifade eden ters fonksiyonu olarak,
• Logaritmanın 1'e gitmesi için kaç kez tekrarlanması gerektiğinin sayısı,
• As a generalization of Robert Munafo's large number class system,
• Biçimsel fonksiyonun bir sınırsız sürümü olarak.

Süper logaritma tanımları

$\,\mathrm{slog}_b(z)$ olarak yazılan süper logaritma, tam olarak şöyle tanımlanır;

$\,\mathrm{slog}_b(b^z) = \mathrm{slog}_b(z) + 1$ ve

$\,\mathrm{slog}_b(1) = 0.$

Bu tanımın sadece tam sayılar verebileceğine ve sadece tam sayı üretebilecek sayıları kabul edebileceğine dikkat edin. Bu tanımın kabul edeceği sayılar $b, b^b, b^{b^b}$ vb. formdadır.

Yaklaşımlar

Genellikle özel fonksiyonlar, argüman(lar)ın reel değerleri için değil, karmaşık düzlem, diferansiyel ve integral ifadeleri içinde tanımlanır. Slag fonksiyonu için mevcut ifadeler olmadığı için, basit yaklaşımlar şöyle öneriliyor.

Süper logaritmaya lineer yaklaşım

Süper logaritmaya lineer yaklaşım şöyledir:

$\mathrm{slog}_b(z) \approx \begin{cases} \mathrm{slog}_b(b^z) - 1 & z \le 0 \mbox{için } \\ -1 + z & 0 < z \le 1 \mbox{için } \\ \mathrm{slog}_b(\log_b(z)) + 1 & 1 < z \mbox{için } \\ \end{cases}$

Bu fonksiyon, tüm reel z ($C^0$ süreklilik) için süreklidir.

İkinci dereceden yaklaşım

Süper logaritmaya ikinci dereceden yaklaşım şöyledir:

$\mathrm{slog}_b(z) \approx \begin{cases} \mathrm{slog}_b(b^z) - 1 & z \le 0 \mbox{için } \\ -1 + \frac{2\log(b)}{1+\log(b)}z + \frac{1-\log(b)}{1+\log(b)}z^2 & 0 < z \le 1 \mbox{için } \\ \mathrm{slog}_b(\log_b(z)) + 1 & 1 < z \mbox{için } \end{cases}$

Bu fonksiyon tüm reel z ($C^1$ süreklilik) için türevlenebilir.

Abel fonksiyonuna yaklaşımlar

Abel fonksiyonu, şu eşitliği sağlayan herhangi bir fonksiyondur:

$\,A_f(f(x)) = A_f(x) + 1$

Verilen bir $A_{f}(x)$ Abel fonksiyonunun diğer çözümü herhangi sabit $A'_{f}(x) = A_{f}(x) + c$ eklenerek elde edilebilir. Verilen bu süper logaritma $\mathrm{slog}_b(1) = 0$ olarak tanımlanır ve üçüncü özelliği üstel fonksiyonun Abel fonksiyonu, eşsiz olarak tanımlanabilmesidir.

Özellikler

Süper logaritmanın diğer eşitlikleri:

$\,\mathrm{slog}_b(z) = \mathrm{slog}_b(\log_b(z)) + 1$

$\,\mathrm{slog}_b(z) > -2$ tüm reel z için

Tetrasyonun tersi olarak slag

Karmaşık z düzlemindeki $f={\rm slog}_{\rm e}(z)$ fonksiyonu.

Tetrasyon olarak $~{\rm sexp}_b(z)~$, analitik fonksiyon olması husunuda şüphelidir. En azından $~b~$'nin bazı değerleri için slog_b=sexp_b^-1 ters fonksiyonu analitik olabilir. Karmaşık z düzlemindeki $~{\rm slog}_b(z)~$'nin davranışı, yukarıdaki şekilde, $~b=e~$ durumu için çizilmiştir. slog fonksiyonunun sanal kısmının reel ve tam sayı değerlerinin dereceleri kalın çizgilerle gösteriliyor.

Ayrıca bakınız

• Ackermann işlevi
• Aşırı işleçler
• Tekrarlı logaritma

Alıntılar

• Daniel Geisler, tetration.org
• Ioannis Galidakis, On extending hyper4 to nonintegers (2006'dan önce) (A simpler, easier to read review of the next reference)
• Ioannis Galidakis , On Extending hyper4 and Knuth's Up-arrow Notation to the Reals (undated, 2006 or earlier).
• Robert Munafo, Extension of the hyper4 function to reals (An informal discussion about extending tetration to the real numbers.)
• Lode Vandevenne, Tetration of the Square Root of Two, (2004). (Attempt to extend tetration to real numbers.)
• Ioannis Galidakis, Mathematics, (Definitive list of references to tetration research. Lots of information on the Lambert W function, Riemann surfaces, and analytic continuation.)
• Galidakis, Ioannis and Weisstein, Eric W. Power Tower
• Joseph MacDonell, Some Critical Points of the Hyperpower Function.
• Dave L. Renfro, Web pages for infinitely iterated exponentials (Compilation of entries from questions about tetration on sci.math.)
• Andrew Robbins, Home of Tetration (An infinitely differentiable extension of tetration to real numbers.)
• R. Knobel. "Exponentials Reiterated." Amerikan Matematik Aylığı 88, (1981), p. 235-252.
• Hans Maurer. "Über die Funktion $y=x^{[x^{[x(\cdots)]}]}$ für ganzzahliges Argument (Abundanzen)." Mittheilungen der Mathematische Gesellschaft in Hamburg 4, (1901), p. 33-50. (Reference to usage of $\ {^{n} a}$ from Knobel's paper.)

Dış bağlantılar

• Andrew Robbins'in tetrasyon sitesi
• Daniel Geisler'in tetrasyon sitesi
• Tetrasyon Forumu
• citizendium'daki tetrasyon