Dalga fonksiyonu
Kuantum fiziğinde dalga fonksiyonu izole bir kuantum sistemindeki kuantum durumunu betimler. Dalga fonksiyonu karmaşık değerli bir olasılık genliğidir ve sistem üzerindeki olası ölçümlerin olasılıklarının bulunmasını sağlar. Dalga fonksiyonu için en sık kullanılan sembol Yunan psi harfidir ψ ve Ψ (Sırasıyla küçük ve büyük psi harfi).

Dalga fonksiyonu, azami bir iletişimli gözlemlenebilirler kümesine karşılık gelen serbest dereceler fonksiyonudur. Belli bir temsiliyet seçildiği sürece dalga fonksiyonu kuantum durumundan türetilebilir.
Belli bir sistemde seçilen iletişimli serbestlik dereceleri özgün veya benzersiz değildir ve karşılıklı olarak fonksiyonun tanım kümesi de özgün veya benzersiz değildir. Örneğin bir konum alanındaki parçacıklarının bütün pozisyon koordinatlarının fonksiyonu olabilir veya bir momentum uzayındaki bütün momentum parçacıkların fonksiyonu olabilir; bu ikisi Fourier dönüşümü üzerinden ilişkilidir. Elektron ve Foton gibi bazı parçacıkların 0 olmayan spinleri vardır ve bu tip parçacıklar için dalga fonksiyonu spini içsel ve ayrı bir serbestlik derecesi olarak alır. İzospin gibi başka değişkenler de alınabilir. Bir sistemin iç serbestlik dereceleri olduğunda sürekli serbestlik derecelerindeki (Uzayda bir nokta) her noktaya dalga fonksiyonu bir karmaşık sayı atar. Bu atama ayrı serbestlik derecelerinin (bkz spinin z-bileşeni) bütün olası değerleri için geçerlidir. Bu değerler genellikle bir sütun matrisinde gösterilirler. (bkz göreli olmayan 1⁄2 spine sahip bir elektron 2 × 1 lik bir sütun vektörü içindir).
Kuantum mekaniğinin süperpozisyon prensibine göre, dalga fonksiyonları birbirleriyle toplanarak veya karmaşık sayılarla çarpılarak yeni dalga fonksiyonları ve karşılığında bir Hilbert uzayı oluşturabilirler. Born kuralı geçiş olasılıklarını iç çarpımlarla ilişkilendirmek için kullanılır. İki dalga fonksiyonu arasındaki iç çarpım karşılıksal fiziksel durumların üst üste gelmelerinin ölçümüdür. Bu kuantum mekaniğinin temel olasılığa dayalı yorumlanmasının yapılması için kullanılır. Schrödinger denklemi dalga fonksiyonlarının zamanla gelişimini belirler ve bir dalga fonksiyonu aynı deniz dalgaları veya ip dalgaları gibi niteliksel olarak davranır çünkü Schrödinger denklemi matematiksel olarak bir dalga denklemidir. Bu dalga fonksiyonu ismini açıklar ve dalga parçacık ikiliğine yol açar. Fakat kuantum mekaniğinde dalga fonksiyonu hala farklı yorumlamalara açık bir fiziksel fenomeni açıklamak için kullanılır. Dalga fonksiyonunun bu özelliği onu klasik mekanikteki dalgalardan ayıran en büyük özelliğidir.[1][2][3][4][5][6]
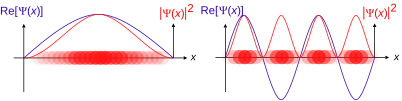
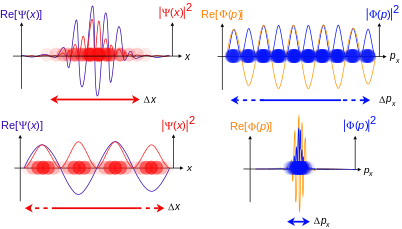
Born'un göreli olmayan kuantum mekaniğindeki istatistiksel yorumunda[7][8] dalga fonksiyonunun modülünün karesi, |ψ|2, gerçek bir sayı verir. Bu gerçek sayı bir parçacığın belirli bir zamanda belirli bir momentuma sahip olmasının veya belirli bir konumda olmasının ölçümünün olasılık genliğini belirtir. Sistemin bütün serbestlik derecelerinde bu değerin integrali olasılık yorumuna göre 1 olmak zorundadır. Bir dalga fonksiyonunun her zaman sağlaması gereken bu gerekliliğe normalleştirme koşulu denir. Dalga fonksiyonu sonuçta karmaşık sayı değerlerine sahip olduğu için sadece göreli evresi ve göreli büyüklüğü ölçülebilir. İzole olarak ele alınırken dalga fonksiyonunun değerleri bize gözlemlenebilir ve ölçülebilir büyüklükler veya yönlerle alakalı hiçbir bilgi vermez. Ölçülebilir miktarların istatistiksel dağılımlarının bulunabilmesi için özdeğerleri olası ölçümlerin kümesine karşılık gelen bir kuantum operatörün dalga fonksiyonu üzerinde kullanılması gerekir.
Tarihçe[değiştir | kaynağı değiştir]
1905 yılında Albert Einstein bir fotonun frekansı ve enerjisi , [9] arasında bir orantılılık olduğunu ve 1916 yılında da bir fotonun itmesi ve dalga boyu , [10]( Planck sabitiyken) arasında bir ilişki olduğunu öne sürdü. 1923'te De Broglie günümüzde "De Broglie İlişkisi" olarak isimlendirilen, formülünün kütleli parçacıklar için de geçerli olduğunu öneren ilk kişi oldu.[11] Bu gelişmeler kuantum mekaniğin modern gelişmesinin başlangıç noktası olarak adlandırılabilirler. Bahsi geçen denklemler kütlesiz ve kütleli parçacıklar için dalga-parçacık ikiliğini temsil ederler.
1920 ve 1930'li yıllarda kuantum mekanik, kalkülüs ve lineer cebirle geliştiriliyordu. Louis de Broglie, Erwin Shrödinger ve kalkülüsten yararlanan diğer bilim insanları dalga mekaniğini geliştirirken, Werner Heisenberg ve Max Born gibi lineer cebir kullananlar ise matris mekaniği üzerinde çalışıyordular. Sonrasında Schrödinger iki yaklaşımın da eşdeğer olduğunu gösterdi.[12]
1926'da Schrödinger, günümüzde Schrödinger denklemi olarak bilinen ünlü dalga denklemini yayımladı. Denklem, kuantum operatörlerini kullanarak klasik enerjinin korunumu ve de Broglie ilişkileri temel alınarak kurulmuştur ve denklemlerin çözümü kuantum sisteminin dalga fonskiyonlarıdırlar. Fakat kimse denklemleri yorumlamayı bilmiyordu.[13] İlk başta Schrödinger ve diğer bilim adamları dalga fonsksiyonlarının dağınık, dalga fonksiyonunun büyük olduğu yerde yoğunlaşan partikülleri temsil ettiğini düşündüler.[14] Fakat bu teori, bir dalga paketinin bir hedeften elastik saçışmasıyla uyumlu değil, her yöne saçılıyordu.[15] Saçılmış bir partikül herhangi bir yöne saçılabilir ancak dağılıp her yöne dağılmaz. 1926'da Born, olasılık genliğini öne sürdü.[15][16][17] Bu, kuantum mekanik hesaplamalarını direkt olarak olasılıksal deneysel gözlemlere bağlıyordu. Olasılık genliği, kuantum mekaniğin Kopenhag yorumunun bir parçası olarak kabul edilir. Kuantum mekaniğin başka birçok yorumu vardır. 1927'de Hartree ve Fock N-Cisim dalga fonksiyonunu çözümleme yolunda ilk adımı attılar ve cevabı yaklaşık olarak bulmak için günümüzde Hartree-Fock metodu olarak bilinen ve bir iteratif algoritma olan öz tutarlılık döngüsünü geliştirdiler.[18] John C. Slater tarafından geliştirilen, Slater Determinantı ve kalıcısı (bir matrisin) metodun bir parçasıydılar.
Schrödinger, dalga fonksiyonu denkleminin göresiz versiyonunu yayınlamadan önce göreli enerji korumasını sağlayan bir versiyonla da karşılaştı fakat olumsuz olasılıkları ve olumsuz enerjileri öngördüğü için dikkate almamayı seçti. 1927'de Klein, Gordon ve Fock da göreli verisyonu buldular ama elektromanyetik etkileşimi de katarak denkelmin Lorentz değişmezi olduğunu kanıtladılar. 1928'de De Broglie de aynı denklemle karşılaştı. Bu göreli dalga denklemi günümüzde Klein-Gordon denklemi olarak biliniyor.[19]
Tanım(tek boyutlu uzayda spinsiz bir parçacık)[değiştir | kaynağı değiştir]
Şimdilik daha basit bir durum olan, tek boyutlu uzaydaki spin'i olmayan ve göreceli olmayan bir parçacığı ele alalım. Daha genel durumlar aşağıda açıklanacaktır.
Konum-uzay dalga fonksiyonları[değiştir | kaynağı değiştir]
Böyle bir parçacığın durumu yalnızca o parçacığın dalga fonksiyonuyla tanımlanabilir,
,
bu fonksiyonda pozisyon ise zamandır. Bu karmaşık-değerli fonksiyon ve değişkenlerine bağlıdır.
1d uzaydaki spinsiz bir parçacık için, dalga fonksiyonu, olasılık genliği olarak yorumlanırsa, dalga fonksiyonunun mutlak değerinin karesi, pozitif gerçel sayı
parçacığın konumundaki olasılık yoğunluğunu verir. Yıldız işareti() fonksiyonun kompleks eşleniğini ifade eder. Parçacığın konumu bilinirse, parçacığın lokasyonu dalga fonksiyonundan belirlenemez, ancak konumunun olasılık dağılımından açıklanabilir.
Normalleştirme koşulu
x olarak betimlenen konumunun a ≤ x ≤ b aralığında olma olasılığı bu aralıktaki yoğunluğun integrali olarak bulunabilir.
Buradaki t parçacığın ölçüldüğü zamanı ifade eder. Buradan normalleştirme koşulu ortaya çıkar:
çünkü eğer parçacık gözlemlendiyse herhangi bir yerde var olma olasılığı 100%dür.
Belirli bir sistemde bütün normalleştirilebilen dalga fonksiyonlarının kümesi (herhangi bir zamanda) soyut matematiksel bir vektör uzayı yaratır. Bu iki farklı dalga fonksiyonun toplanabileceği ve hatta karmaşık sayılarla çarpılabilecekleri anlamına gelir. Teknik olarak normalleştirme koşulu yüzünden dalga fonksiyonları normal bir vektör uzayı yaratmaktansa projektif bir uzay yaratırlar. Bu vektör uzayı sonsuz boyutludur çünkü farklı kombinasyonlarla toplananınca mümkün olan bütün fonksiyonları üretebilecek sonlu bir fonksiyon kümesi yoktur. Ayrıca bu bir Hilbert uzayıdır çünkü iki dalga fonksiyonu Ψ1 ve Ψ2'nin iç çarpımı karmaşık sayı olarak tanımlanabilir. (t zamanında)
İki dalga fonksiyonunun iç çarpımı her ne kadar bir karmaşık sayı olsa da bir dalga fonksiyonunun kendisi ile olan iç çarpımı,
her zaman bir pozitif gerçek sayıdır. ||Ψ|| sayısı (||Ψ||2 değil) bir dalga fonksiyonunun normudur.
Eğer (Ψ, Ψ) = 1 sağlanıyorsa o zaman Ψ is normalleşmiştir. Eğer Ψ normalleşmemişse, kendisini normuna bölmek normalleşmiş fonksiyonu verir Ψ/||Ψ||. Eğer (Ψ1, Ψ2) = 0 ise bu iki dalga fonksiyonu ortogonaldir. Eğer hem normalleşmiş hem de otrogonalseler o zaman otronormaldirler. Ortogonalite ve ortonormalite dalga fonksiyonlarının sahip olması gereken zorunlu koşullar değillerdir fakat göz önünde bulundurması faydalı kavramlarıdr çünkü bu foksiyonların doğrusal bağımsızlıklarını garantilerler. Ortogonal dalga fonksiyonlarının Ψn doğrusal kombinasyonlarında aşağıdaki durum olur,
Eğer dalga fonksiyonları ortogonal olmasaydı katsayıları elde etmek daha karmaşık olurdu.
Vektörel olarak kuantum durumları
Kopenhag yorumlamasında, iç çarpımın (karmaşık bir sayı) modülünün karesi gerçel bir sayı verir.
Eğer iki fonksiyon da normalleştirilmişse bu sayı bir Ψ2 fonksiyonunun yeni bir Ψ1 fonksiyonuna çökme olasılığını verir. Bu Born kuralıdır[7] ve kuantum mekaniğinin temel varsayımlarından bir tanesidir.
Zamanın belirl bir noktasında Ψ(x, t) dalga fonksiyonunun tüm değerleri bir vektörün bileşenleridir. Bu vektörlerden sonsuz tane vardır ve toplama yerine entegrasyon kullanılır. Bra-ket gösteriminde vektör aşağıdaki gibi gösterilir,
ve bir "kuantum durum vektörü" olarak adlandırılır (ya da basitçe bir kuantm durumu). Dalga fonksiyonlarını soyut bir vektör uzayını temsil edicek şekilde düşünmenin birkaç avantajı vardır:
- Lineer cebirin bütün araçları dalga fonksiyonlarını anlamak ve manipüle etmek için kullanılabilir. Örneğin:
- Lineer cebir bir vektör uzayının bir baz olarak nasıl ifade edilebileceğini açıklar. Sonrasında vektör uzayındaki herhangi bir vektör bu baz içerisinde ifade edilebilir. Bu konum uzayındaki bir dalga fonksiyonu ile momentum uzayındaki bir dalga fonksiyonu arasındaki ilişkiyi göstermek için kullanılabilir.
- Bra-ket gösterimi dalga foksiyonlarını manipüle etmek için kullanılabilir.
- Kuantum durumlarının soyut bir vektör uzayında vektör olmaları kuantum mekaniği ve kuantum dalga kuramının bütünü için doğru sayılabilecek genel bir fikirdir. Fakat kuantum durumlarının uzaydaki karmaşık değerli "dalga" fonksiyonlaı olması sadece belirli durumlarda geçerliliğini korur.
Zaman parametresi genelde bastırılır ve aşağıdakilerde olacaktır. x koordinatı sürekli bir indekstir. |x⟩ler baz vektörlerdir ve ortonormallerdir yani iç çarpımları bir delta fonksiyonudur;
yani
ve
bu da kimlik operatörünü açığa çıkarır.
Bir bazdaki kimlik operatörünü bulmak soyut durumun baz içinde açıkça ifade edilmesini sağlar. (iki durum vektörünün iç çarpımları ve gözlemlenebilirler için diğer operatörler baz içerisinde ifade edilebilir).
Momentum-uzay dalga fonksiyonları[değiştir | kaynağı değiştir]
Parçacık momentum uzayında da bir dalga fonksiyonuna sahiptir.
burada p tek boyutta momentumu ifade eder ve −∞ ile +∞ arasındaki herhangi bir değeri alabilir. t ise zamandır.
Konum durumuna benzer şekilde Φ1(p, t) ve Φ2(p, t) olarak ifade edilen iki dalga fonksiyonunun iç çarpımları aşağıdaki gibi ifade edilebilir,
Zamandan bağımsız Schrödinger denkleminin bir çözümü aşağıdaki gibidir,
Momentum operatörünün özfonksiyonu olduğu için tam olarak p momentumuna sahip bir parçacığı betimlemek için kullanılabilen bir düzlem dalgası. Bu fonksiyonlar birlik olucak şekilde normalleştirilemezler (kare-entegre edilebilir değillerdir), yani fiziksel Hilbert uzayının elementleri değillerdir. Aşağıdaki küme,
momentum bazı adı verilen bir şeyi oluşturur. Bu "baz" matematiksel anlamdaki bir baz değildir. Öncelikle, bu fonksiyonlar normalleştirilebilir olmadıkları için, bir delta fonksiyonuna normalleştirilirler,
İkincil olarak, lineer olarak bağımsız olsalar bile fiziksel bir Hilber uzayının bazı için onlardan çok fazla vardır (sonsuz bir küme oluştururlar). Daha sonra açıklanacağı üzere Fourier dönüşümü üzerinden diğer bütün fonksiyonları açıklamak için kullanılabilirler.
Konum ve momentum gösterimleri arasındaki ilişki[değiştir | kaynağı değiştir]
x ve p gösterimleri aşağıdaki gibidir,
İki denklemdeki son iki ifadeyi kullanarak Ψ konumunun momentum özfonksiyonlarına projeksiyonları alındığında aşağıdaki ifadelere ulaşılır,[20]
Serbest Schrödinger denkleminin konum temsilli çözümlerindeki uygun şekilde normalleştirilmiş momentum özdurumlarının bilinen ifadeleri kullanıldığında,
elde edilen,
Benzer bir şekilde konumun özfonksiyonu kullanıldığında,
Bunlar ele alındığın konum-uzay ve momentum-uzay dalga fonksiyonlarının birbirlerinin Fourier dönüşümleri oldukları ortaya çıkar.[21] İki dalga fonksiyonu da aynı bilgiyi taşırlar ve ikisinden herhangi biri de parçacığın bütün bilgilerini hesaplamak için yeterlidir. Bunlar elementleri değerlendirme altındaki bir sistemin olası durumları olan soyut fiziksel Hilbert uzaylarının elementlerini temsil ettiklerinden aynı durum vektörlerini temsil ederler, yani aynı fiziksel durumu. Fakat kare-integrallenebilir fonksiyonlar olarak bakıldığında genelde eşit değillerdir.
Uygulamada, konum-uzay dalga fonksiyonu momentum-uzay dalga fonksiyonundan çok daha fazla kullanılır. Gerekli denklemin (Schrödinger, Dirac, vb.) potansiyel eklenişi hangisinin daha kolay olduğunu belirler. Harmonik osilatör için, x ve p simetrik olarak girer yani hangi tanımın kullanıldığı çok da fark etmez. Aynı denkleme (modula sabitleri) ulaşılır. Bundan bir uydurmaya ulaşılabilir. Harmonik osilatörünün dalga fonksiyonunun sonuçları L2 deki Fourier dönüşümünün özdeğerleridir.
Tanımlar (diğer durumlar)[değiştir | kaynağı değiştir]
Aşağıdakiler dalga fonksiyonunun yüksek boyutlar ve çoklu parçacık sistemlerindeki genel halleridir. Ayrıca farklı serbestlik derecelerine ve konum ile momentum bileşenleri dışındaki bileşenlere de sahiptirler.
3d konum uzayında tek parçacıklı durumlar[değiştir | kaynağı değiştir]
3 uzaysal boyutta spinsiz bir parçacığın konum-uzay dalga fonksiyonu şu ana kadar gösterilen tek uzaysal boyuttakine benzerdir,
r burada üç boyutlu uzaydaki bir konum vektörüdür ve t zamanı temsil eder. Her zamanki gibi gerçel değişkenli karmaşık değerli bir fonksiyondur. Dirac gösterimiyle tek vektör,
Daha önceden iç çarpım, momentum-uzay dalga fonksiyonları,Fourier dönüşümleri... ile ilgili bahsedilen lerin hepsi bir üst seviyedeki uzaysal boyut için de aynı şekilde geçerlidir.
Konum serbestlik dereceleri göz ardı edilince spinli bir parçacık için dalga fonksiyonu sadece spinin fonksiyonudur (zaman bir parametredir);
sz z-ekseninde spin projeksiyon kuantum sayısıdır. (z-ekseni rastgele bir seçimdir dalga fonksiyonu gerekli şekilde dönüştürülürse diğer eksenler de kullanılabilir.) sz parametresi, r ve t aksine, ayrık bir değişkendir. Örneğin 1/2 spinli bir parçacık için sz sadece +1/2 ya da - 1/2 olabilir. Bütün kuantum sayılarının eklenmesi uzay-zamanın ilginç bir karmaşık değerli fonksiyonunu verir. Bunlardan 2s+1 tane vardır ve sütun vektörü olarak sıralanabilirler.
Kaynakça[değiştir | kaynağı değiştir]
- ^ Camilleri, Kristian. (2009). Heisenberg and the interpretation of quantum mechanics : the physicist as philosopher. Cambridge: Cambridge University Press. ISBN 978-0-521-88484-6. OCLC 244767751.
- ^ Born, M. (1 Mart 1927). "Physical Aspects of Quantum Mechanics". Nature (İngilizce). 119 (2992): 354-357. doi:10.1038/119354a0. ISSN 1476-4687. 29 Temmuz 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Aralık 2020.
- ^ Murdoch, Dugald. (1987). Niels Bohr's philosophy of physics. Cambridge [England]: Cambridge University Press. ISBN 0-521-33320-2. OCLC 15791648.
- ^ Broglie, Louis de (1960). Non-linear wave mechanics, a causal interpretation;. Internet Archive. Amsterdam, New York, Elsevier Pub. Co.
- ^ Landau, L. D. (Lev Davidovich), 1908-1968,. Quantum mechanics : non-relativistic theory. Third edition, revised and enlarged. Landau, L. D. (Lev Davidovich), 1908-1968,, Lifshit︠s︡, E. M. (Evgeniĭ Mikhaĭlovich),, Pitaevskiĭ, L. P. (Lev Petrovich),, Sykes, J. B. (John Bradbury),, Bell, J. S.,. Oxford. ISBN 0-08-020940-8. OCLC 2284121.
- ^ Newton, Roger G. (2002). Quantum physics : a text for graduate students. New York: Springer. ISBN 0-387-95473-2. OCLC 49351321.
- ^ a b Born, Max (1 Aralık 1926). "Zur Quantenmechanik der Stoßvorgänge". Zeitschrift für Physik (Almanca). 37 (12): 863-867. doi:10.1007/BF01397477. ISSN 0044-3328.
- ^ "Max Born", Wikipedia (İngilizce), 8 Aralık 2020, erişim tarihi: 11 Aralık 2020
- ^ Arons, A. B.; Peppard, M. B. (Mayıs 1965). "Einstein's Proposal of the Photon Concept—a Translation of the Annalen der Physik Paper of 1905". American Journal of Physics. 33 (5): 367-374. doi:10.1119/1.1971542. ISSN 0002-9505.
- ^ EINSTEIN, A. (1967), "On the Quantum Theory of Radiation", The Old Quantum Theory, Elsevier, ss. 167-183, ISBN 978-0-08-012102-4, erişim tarihi: 4 Aralık 2020
- ^ DE BROGLIE, LOUIS (Ekim 1923). "Waves and Quanta". Nature. 112 (2815): 540-540. doi:10.1038/112540a0. ISSN 0028-0836.
- ^ Hanle, Paul A. (Aralık 1977). "Erwin Schrödinger's Reaction to Louis de Broglie's Thesis on the Quantum Theory". Isis. 68 (4): 606-609. doi:10.1086/351880. ISSN 0021-1753.
- ^ Tipler, Paul A.; Mosca, Gene (2009). "Physik". doi:10.1007/978-3-8274-2236-1.
- ^ Weinberg, Steven, 1933- (2013). Lectures on quantum mechanics. Cambridge: Cambridge University Press. ISBN 978-1-107-02872-2. OCLC 798059420.
- ^ a b Wheeler, John Archibald; Zurek, Wojciech Hubert, (Ed.) (31 Aralık 1983), "Frontmatter", Quantum Theory and Measurement, Princeton: Princeton University Press, ss. i-iv, ISBN 978-1-4008-5455-4, erişim tarihi: 11 Aralık 2020
- ^ BORN, M. (1968), "Quantum Mechanics of Collision Processes", Wave Mechanics, Elsevier, ss. 206-225, ISBN 978-0-08-203204-5, erişim tarihi: 11 Aralık 2020
- ^ Young, Hugh D. (2008). Sears and Zemansky's University physics : with modern physics. 12th ed. Freedman, Roger A., Ford, A. Lewis (Albert Lewis), Sears, Francis Weston, 1898-1975. San Francisco: Pearson Addison Wesley. ISBN 0-321-50121-7. OCLC 166268535.
- ^ Atkins, P. W. (Peter William), 1940- (1974). Quanta : a handbook of concepts. Oxford: Clarendon Press. ISBN 0-19-855493-1. OCLC 1257229.
- ^ Martin, B. R. (Brian Robert) (2008). Particle physics. 3rd ed. Shaw, G. (Graham), 1942-. Chichester, UK: Wiley. ISBN 978-0-470-03293-0. OCLC 230916885.
- ^ Shankar, Ramamurti. (1994). Principles of quantum mechanics. 2nd ed. New York: Plenum Press. ISBN 0-306-44790-8. OCLC 30811075.
- ^ Griffiths, David J. (David Jeffery), 1942- (2005). Introduction to quantum mechanics. 2nd ed. Upper Saddle River, NJ: Pearson Prentice Hall. ISBN 0-13-111892-7. OCLC 53926857.